Hi, I cluster eras by analyzing how well you can predict an era by overfit another era.
The idea is: If you have an overfitted model to an era A and it is good at predicting an era B, then A and B should be similar.
How I do it:
- Create one model per era and train it only on its era.
- With every model predict every era.
- Measure the correlations between the predictions and targets.
- Create a matrix where each row is made of model correlations.
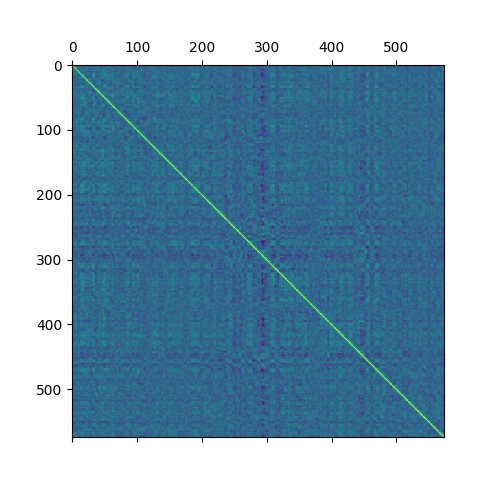
The matrix of correlations between eras sorted by era number:
After a little bit of preprocessing and dimensionality reduction I cluster them.
I played with different number of clusters and came up with 5,3, and lastly 4 being the best.
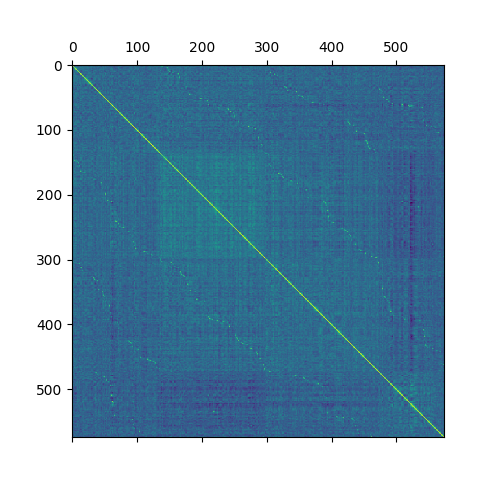
The next picture has same values as the first one, but now its sorted by cluster and number of an era within a cluster. That’s why you can see square patterns (clusters), and the waves across the squares (eras tend to be similar to eras that are timewise close to them)
I am currently working on a model that would harvest this knowledge, so far it was better to use era boosting method. The era boosting method does a similar thing, but it better targets the weaknesses of a little-meta model. With the new data I have more success but the computations take a lot of time, I hope it will be worth it at the end :).
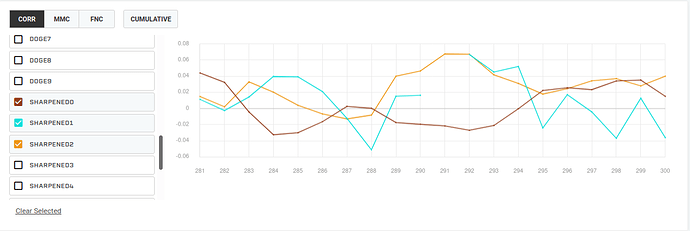
I trained 3 models on 3 clusters (now I use 4) separately to see how they would do over time, and it seems that they nicely complement each other; therefore, if I am able to guess when to use which…
Now I am working on meta model that would predict which era is which, thus would not need a target to classify tournament eras.