We agree that payouts have to be limited in the future to stop exponential growth. It might help if, in the future, payouts were better aligned with actual fund performance. A short term solution of refocusing efforts on Signals is a red herring. It simply does not face the issue at hand. In the mean time an overall proration scheme has a negative effect on attracting unique models. In recent history all models went through “an inflationary phase” to borrow a term in astrophysics. What the team should prefer to do is replicate that experience for all relative newcomers, because its exciting for the newcomer and it is also healthier for the Hedge Fund. A way to do that is introduce an individual stake dependent cutoff factor. The problem of duplicating accounts to try to get around the individual stake limitation factor can be easily fixed by introducing another correction factor which is simply a function of the maximum correlation of a submission to any other prediction submitted in a round, i.e., (1-\max C_{ij}). Then the payout would be
\mathrm{payout}_i = \frac{ \mathrm{Stake}_i}{1+\frac{15\times \mathrm{Stake}_i}{300\mathrm{K\ NMR}}} \mathrm{Corr}_i \times \left(1-\max C_{ij}\right).
As a replacement for MMC, a payout system using the above payout formula would encourage more unique models by giving new modelers an exponential boost that is not gamable. What is also nice about this is that it is more deterministic and much easier to calculate than MMC.
5 Likes
this is gameable and discourages new participation because as the number of submission increases, a model’s corr with any other model is more likely to increase. More participants = lower payout but NOT necessarily that more stakes = lower payout.
3 Likes
Its already been shown that MMC decreases as new models come in, thus the reason for the implementation of a constant multiplier on the MMC. Except MMC is not considered gaming and its true that its not. New models coming into the tournament is not gaming, its just a natural process. The difference between MMC and the present proposal are the factors that explicitly take into account individual stake in order to inhibit exponential growth and the fact that this calculation is much simpler than MMC and is not gamable. The game whereby someone waste efforts into producing low staked models similar to those of other contestants is very likely not a Nash Equilibrium point.
1 Like
I would like to add one more aspect to the discussion, which I think also fits the title of the topic.
Unlimited staking leads to exponential grwoth of payouts, at least so long you can earn more per invested money at outside in the real market.
So long for corr is paid, everyone can submit and stake on example(-like) predictions, wich is easy to create, even for beginners and non data-scientist.
The more money you have the more you can earn, without any or less contribution to the meta-model even in the case of negative impact.
This may a part of the reasons why MMC was introduced and I think it does a good work.
I would go a step further.
I would suggest to apply the payout cap for corr and mmc separatly.
And MMC-payout should be get more weigth.
For my opinion it can be hold simple and easy and transparent for all.
for example:
Corr payout-factor will be limited to 300 000 NMR so at is planned and calculated now.
Define a suitable MMC-stake_cap.
calculate the MMC-payoutFactor as
MMC_payoutFactor = max(1, MMC-Stake_Cap / (0.5 * Staked_1/2MMC + 1.0 Staked_MMC + 2* Staked_2MMC))
where
Staked_1/2MMC = total amount of stakes with MMC-stake-option 1/2 MMC
Staked_MMC = total amount of stakes with MMC-stake-option MMC
Staked_2MMC = total amount of stakes with stake-option 2 MMC
So, the global cap will be stay limited.
But the (expected) exponential growth of staking on Corr will at first (and I believe for long time) not hurt MMC-payout.
I believe, it would be good for the competition to pay more for hard work than for easy work.
And it would be good for the numerai-eco-system to pay more for models which lead to a positive contribution to the meta-model instead of
supporting high staked and easy to create example clones or mainstream models.
1 Like
I think you are correct that whatever form the limiting function takes, it should explicitly take into account MMC. In a bit I will describe a modification of the formula that I presented that does so and it also smoothly transitions from the actual (present) formulation of the payout to the system that I am proposing that gives new-comers a better chance to contribute positively to the meta-model without being gamable.
I have some results from a toy simulation utilizing the actual payout function.
TL;DR: Things are much better than I had hypothesized: Newer good models can catch up to older high staked models, but it takes time.
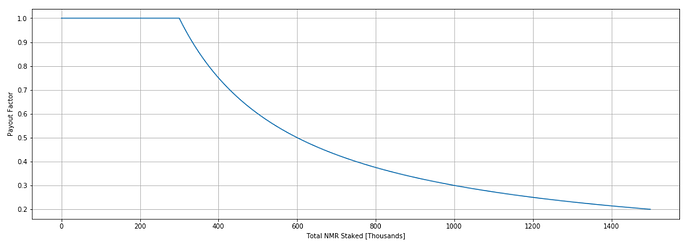
First, l check to see if I understand prorating. You can compare the below plot to the docs. They are pretty much the same. So, I do.
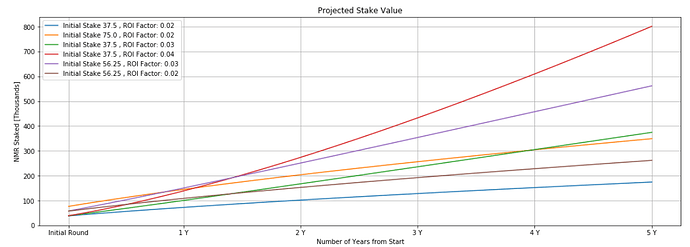
Next, toy simulation results:
The toy simulation starts with 6 models with different combinations of initial stake values and ROI factors. The ROI factor is corr * corr_multiplier + mmc * mmc_multipier used in the actual payout formula. The sum of the initial stake for all of the models is 300 K NMR.
Now looking at the results for my conservative values of the ROI factor chosen you can get a sense of what is going to happen. The spread of initial values shown here is tiny compared to the actual range of initial values in the actual tournament. So this toy is illustrative of the fact that It can take a very long time for superior models to catch up to high staked models. But they can.
Given this exercise I am feeling much better about the effect of proration. I don’t believe the other reasons I have heard for days now against the proposal I presented here were decisive in knocking it down, but now that I see these results I believe the actual situation is pretty good. For that reason unless anyone else can imagine any other reason for this proposal I will withdraw it.
Note that there is a plot in the docs very similar to my 2nd plot here and it makes no sense in the present context. You won’t see growth like that because of the proration function. Growth will look more like these curves.
Congratulations team and @richai .
1 Like
I think the most simple and effective way of apply the payout factor is do it over the total amount stacked by each person using a threshold of a few thousands of NMR.
Currently a few whales are causing the payout falls quickly, and they will colapse the system in few months. Meanwhile if someone with a good model begins the play with a small stack of 500 NMR or so, the impact in the weighted model will be minimal, and the potential return in absolute terms of NMR too.
The whales are not good for Numerai nor the community and will cause the collapse soon. A limit of the stacking per person is necessary, otherwise the weighted stacked model will be the average of a few whales models.
3 Likes
I think we agree that those with higher stakes should take the brunt of the payout penalty. The problem is where do you make the cut? Whatever criteria that you use can be argued. According to Dawkins we have Plato to blame for the curse of Essentialism – the knee-jerk effort to put things into categories (I know this statement is ironic when said to a bunch of data scientists whose job is to put things into categories). That’s why I think that my proposal is better – it avoids a meaningless argument; regression makes more sense than categorical placement. The method I have described is not easy to game, especially given that moving large amounts of crypto around generates tax events. The more I think about this proposal the more I think it is a good idea again, especially given that Numerai seems to have little interest to link Hedge Fund performance to NMR price via NMR buybacks on the open market.
1 Like